Mới 2023: Giải bài 1,2,3 ,4,5,6 ,7,8 trang 153,154,155 Đại số lớp 10: Công thức lượng giác

Bài 3 Chương 6 – Công Thức Lượng Giác: Giải bài 1 trang 153; Bài 2, 3, 4, 5, 6 trang 154; bài 7,8 trang 155 SGK Toán Đại số 10.

Đầu tiên. công thức cộng

cos(a – b) = cosacosb + sinasinb

cos(a + b) = cosacosb – sinasinb

sin(a – b) = sinacosb – sinbcosa

sin(a + b) = sinacosb + sinbcosa

Bài 1. tính toán

a) cos225⁰ tội lỗi 240⁰ Giường cũi (-15⁰ ), nóng chảy 75⁰ ;

Trả lời: a) + cos225⁰ = cosin(180⁰ + 45⁰ ) = -cos45⁰ = -√2/2

+ tội 240⁰ = tội lỗi(180⁰ + 60⁰ ) = -sin60⁰ = -√3/2

+ cũi(-15⁰ ) = -cot15⁰ = -tan75⁰ = -tan(30⁰ + 45⁰ )

---

Bài 2. a) cos(α + π/3), biết rằng sinα = 1/√3 và 0 < α < π/2.

b) tan(α – /4), biết cosα = -1/3 và /2< α

c) cos(a + b), sin(a – b), biết sina = 4/5, 0⁰ 0 Và tội lỗi b = 2/3, 90⁰ < b < 180⁰

---

Bài 3 trang 154. biểu thức đơn giản hóa

a) sin(a + b) + sin(π/2 – a)sin(-b).

b) cos(π/4+ a)cos(π/4 – a) + 1/2 sin²MỘT

c) cos(π/2 – a)sin(π/2 – b) – sin(a – b)

trả lời:

---

Bài 4. chứng minh đẳng thức

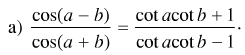
b) sin(a + b)sin(a – b) = sin²tội²b = cosin²b-cosine²MỘT

c) cos(a + b) cos(a – b) = cos²tội²b = cosin²b – tội lỗi²MỘT

Giải pháp 4:

Lưu ý rằng có thể biến mặt phải thành mặt trái

b) VT = [sinacosb + cosasinb][sinacosb – cosasina]

= (sinacosb)² – (cosasinb)² = ác² a(1 – tội lỗi² b) – (1 – tội lỗi² a) tội lỗi² Thứ hai

= ác²tội²b = cosin²b( 1 – cosin²a) – cosin² a(1 – cosin² b) = cosin²b-cosine²MỘT

c) VT = (cosacosb – sinasinb)(cosacosb + sinasinb)

= (cosacosb)² – (sinasinb)²

= cosin² a(1 – tội lỗi² b) – (1 – cosin² a) tội lỗi² b = cosin² tội² Thứ hai

= cosin² b(1 – tội lỗi² a) – (1 – cosin² b) tội lỗi² a = cosin² b – tội lỗi² MỘT

---

Bài 5. Tính sin2a, cos2a, tan2a, biết:

a) sina = -0,6 và π < a < 3π/2;

b) cosa = -5/13 và /2 < a

c) sina + cosa = 1/2 và 3π/4 < a < π

phần thưởng: a) sina = -0,6 và π < a < 3π/2;

b) cosa = -5/13 và /2 < a

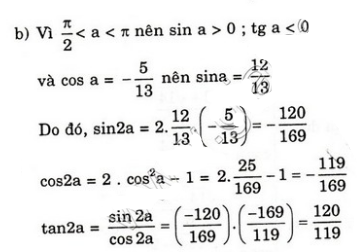
c) sina + cosa = 1/2 và 3π/4 < a < π

---

Bài 6. Đặt sin 2a = -5/9 và π/2 < a < π.

Tính sina và cosa.

---

Trang 155 Bài 7. Chuyển tích của các biểu thức sau

a) 1–sinx b) 1 + sinx;

c) 1+2cosx d) 1-2sinx

a) 1 – sinx

b) 1 + sinx

c) 1 + 2cosx

d) 1-2 sinx

---

Bài 8. Rút gọn biểu thức A

hướng dẫn: Ta có: sinx + sin3x + sin5x = sinx + sin5x + sin3x

= sin3x(2cos2x + 1) (1)
– cosx + cos3x + cos5x = cosx + cos5x + cos3x
= 2cos3x. cos2x + cos3x = cos3x(2cos2x + 1) (2)

Từ (1) và (2) ta có:

Vậy A = tan3x.